Wstęp
Sondy pola elektrycznego używane na co dzień w laboratoriach EMC lub przez inżynierów działów R&D są urządzeniami często niedocenianymi przez użytkowników. Dla inżyniera często liczy się tylko zakres częstotliwości, czyli zakres w jakim może wykonać rzetelne pomiary pola elektrycznego np. w zakresie od 9 [MHz] do 18 [GHz] oraz dynamiczny, czyli zakres w jaki może wykonać rzetelne pomiary natężenia pola elektrycznego np. od 1 [V/m] do 1000 [V/m] takiego produktu w codziennych pomiarach.
Inne wymagania to szybkość próbkowania takiej sondy oraz rozdzielczość pomiarowa. Oprócz tych dwóch parametrów, jednym z bardziej niedocenianych, jest izotropowość sondy pola. Przedyskutujemy ten temat w tym artykule.

Izotropowość sondy – Podstawowe definicje
Izotropia to własność sondy pola elektrycznego do poprawnego pomiaru pola niezależnie od orientacji sondy w generowanym polu elektromagnetycznym. Sonda pola z idealną odpowiedzią izotropową powinna więc wskazywać ciągle na te same wartości (w [V/m]) niezależnie od jej orientacji, a graficzna reprezentacja zmierzonego pola będzie idealnym okręgiem. W praktyce nie wszystkie sondy pola cechują się izotropowością. Dzieje się tak z wielu powodów z wielu powodów, może to byż spowodowane np. kształtem anten sondy pola.
Zdefiniujmy jeszcze jednorodność pola i anizotropowość. W przypadku jednorodności jest to własność i kryterium jakości komory bezodbiciowej EMC. W idealnie wykonanej komorze EMC (bez odbić i bez fal stojących) pole jest jednorodne (jest takie same) w każdym miejscu obiektu. Jednakże komory EMC są obiektami rzeczywistymi i tego typu sytuacje są rzadkie. Wpływa to na wyniki pomiarów pola elektrycznego z użyciem sond pola. W celu zmierzenia tej własności korzysta się z metody pomiarowej zgodnie z IEC 61000-4-3 Ed. 3.1 b lub EN 61000-4-3. Pomiaru dokonuje się w 16 punktach pionowej płaszczyzny o wymiarach 1,5 [m] x 1,5 [m]. Jednorodność w tym przypadku musi mieścić się w błędzie maksymalnym +-6 [dB].
Anizotropowość można zdefiniować jako odwrotność izotropowości. Ciekawym przykładem może być mikrofalowe promieniowanej tła (rysunek 1). Zgodnie z normą IEEE-std 1309-2013 anizotropowość definiuje się wzorem:
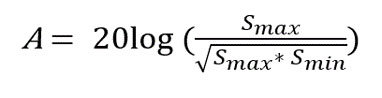
gdzie:
- Smax i Smin – zmierzona amplituda pola elektrycznego w [V/m] dla konkretnej orientacji sondy pola.
Należy również przypomnieć jak mierzone są wartości Smax i Smin z równania. W przypadku sondy pola z 3 antenami (oś X, Y oraz Z) efektywną wartość mierzonego pola uzyskuje się stosując wzór:
gdzie:
− 𝑬x - Pomiar amplitudy pola z osi X sondy pola,
− 𝑬y - Pomiar amplitudy pola z osi Y sondy pola,
− 𝑬z - Pomiar amplitudy pola z osi Z sondy pola.
Wartość więc ta jest odpowiednikiem parametru Smax i Smin dla całościowej anizotropii. W tym momencie też możemy zaaplikować wartości korekcyjne dla poszczególnych osi.
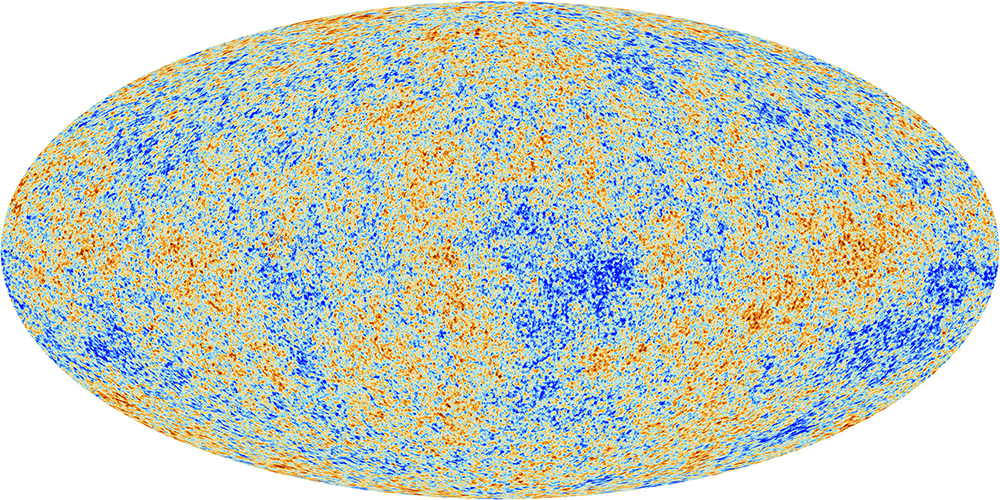
Rysunek 1. Anizotropowość pomiaru promieniowania kosmicznego podczas wielkiego wybuchu.
Parametry wpływające na izotropię
W przypadku sond pola elektrycznego jednym z ważnych parametrów jest ich budowa. Na początku w pierwszej generacji sondy pola posiadały tylko 3 elementy (rysunek 2), w drugiej generacji zwiększono ilość anten do 6 elementów (rysunek 3).

Rysunek 2. Prototypy pierwszych sond pola elektrycznego.

Rysunek 3. Nowoczesna sonda pola z 6 elementami antenowymi.
Kilka parametrów wpływających na anizotropię:
- Kształt obudowy sondy - może wpływać na niejednorodność pola wokół sondy pola.
- Budowa anteny sondy pola - kształt anteny oraz dopasowanie impedancyjne względem pola.
- Symetryczność sondy pola - ten parametr może być osiągnięty jedynie przez sondy pola z 6 antenami.
- Sposób montażu sondy pola, statyw i system montażowy.
Dodatkowo na izotropię wpływa też rozmiar i umieszczenie elementów antenowych w sondzie pola. Poniższa tabelka (tabela 1) przedstawia dwie rodzaje sondy i wpływ parametrów na izotropowość. Sonda mała ma elementy antenowe umieszczone w bliskiej odległości od elektroniki. W przypadku drugim elementy antenowe są odsunięte od elektroniki na daną odległość.
| Sonda mała | Sonda z antenami na pałąku |
|---|---|
| Mała sonda pola | Długi pałąk |
| Dystans pomiędzy elementami jest duży | Dystans pomiędzy elementami jest mały |
| Duży wpływ obudowy sondy na mierzone wartości pola dla wysokich częstotliwości | Mały wpływ obudowy sondy na mierzone wartości pola |
| Dobre działanie sondy dla niskich częstotliwości (od 9 [kHz]) | Słabe działanie sondy dla niskich częstotliwości (od 10 [MHz] typowo) |
| Dobra izotropowość może być osiągnięta, ale należy wziąć pod uwagę niektóre czynniki | Bardzo dobra izotropowość sondy pola |
Tabela 1. Sonda mała vs sonda z pałąkiem.
Warto jeszcze wspomnieć o jednym z powodów, dla których izotropowość jest zmienna w przypadku różnej budowy sond. Dla niskich częstotliwości długość fali jest duża i nie wpływa ona na pomiary dla małych urządzeń. Problem pojawia się w przypadku wysokich częstotliwości, gdzie długość fali jest mała. Przykładowo:
LF = V/F1 = 299792458/50000000 ~ 6 [m]
HF = V/F2 = 299792458/6000000000 ~ 0,05 [m]
gdzie:
- LF – długość fali dla niskiej przykładowej częstotliwości [m],
- HF – długość fali dla wysokiej przykładowej częstotliwości [m],
- V – prędkość światła około 299792458 [m/s],
- F1 – częstotliwość 50 [MHz],
- F2 – częstotliwość 6 [GHz] .
Metody pomiarowe izotropii
Przyjrzyjmy się dwóm metodom pomiaru anizotropii. Pierwsza z nich została zdefiniowana w normie IEEE-std 1309-2015. Polega ona na obrocie sondy pola o 360 stopni, przy specyficznym ułożeniu samej sondy pola pod kątem 54,7 stopni (rysunek 4 i 5). Stosując tę metodą podczas obrotu sondy każda z osi (X, Y oraz Z) będą znajdować się równolegle do pola.
Wynik tego typu pomiarów może być przedstawiony w postaci wykresu biegunowego.
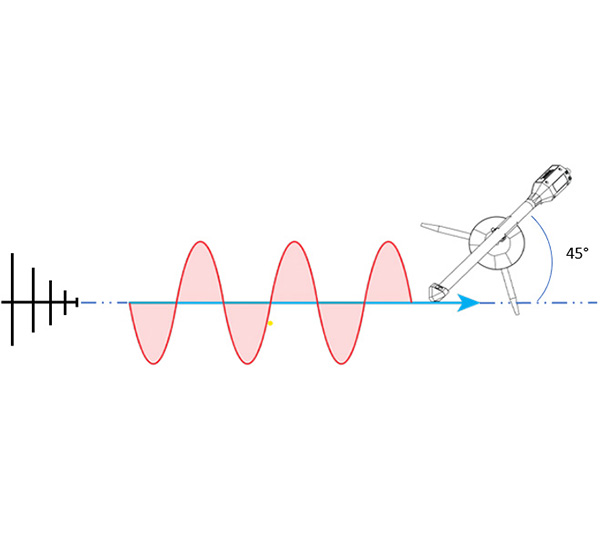
Rysunek 4. Układ sondy pola w metodzie pierwszej.
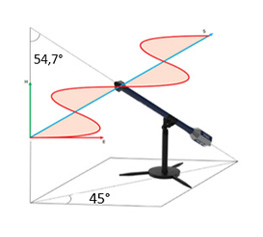
Rysunek 5. Sonda pola. Rzut z boku.
Jak już wspomniano, istnieje również druga metoda pomiarowa. W tej metodzie sondę pola obracamy wzdłuż płaszczyzny poziomej, generując pole elektryczne spolaryzowane również poziomo. W tym przypadku tylko dwie osie będą narażone polem elektrycznym. Jedna z nich będzie zawsze skierowana prostopadle i nie będzie pokazywać nic.
Dla metody pierwszej możemy zdefiniować wykresy biegunowe. Przypadek idealny jest przedstawiony poniżej (rysunek 6).
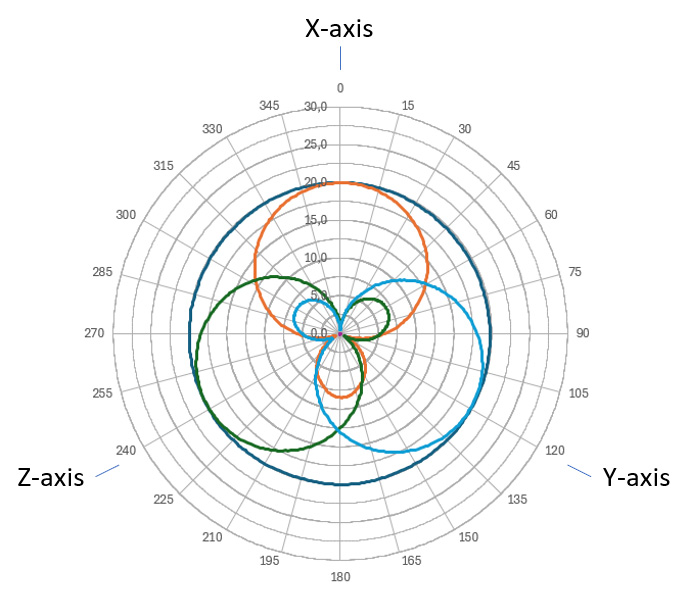
Rysunek 6. Idealny przypadek pomiarów na wykresie biegunowym.
Dla drugiej metody, autorzy poniżej przedstawiają w sumie trzy wykresy biegunowe. Są one wykonane dla częstotliwości 1 [GHz]. Pierwszy z nich przedstawia pomiary w płaszczyźnie i polaryzacji poziomej. Drugi płaszczyzna pozioma i polaryzacja pionowa. Trzeci przedstawia przypadek skierowania wszystkich osi w górę. Ten pomiar ma też pewne wady:
- nie wszystkie osie są mierzone,
- wynik pokazuje jedynie anizotropię 2D. Anizotropia 3D jest naszym „najgorszym przypadkiem”,
- wpływ mocowania sondy pola,
- wpływ stołu obrotowego,
- wpływ niejednorodności pola komory EMC,
- częstotliwość 1 [GHz].
Legenda:
- kolor żółty – całościowy pomiar,
- kolor niebieski – Oś X,
- kolor czerwony – Oś Z,
- kolor zielony – Oś Y.
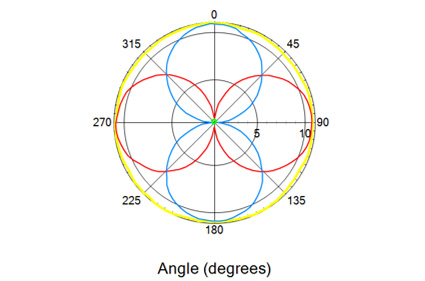
Rysunek 7. Wykres dla rotacji płaszczyźnie i w polaryzacji poziomej Częstotliwość 1 [GHz].
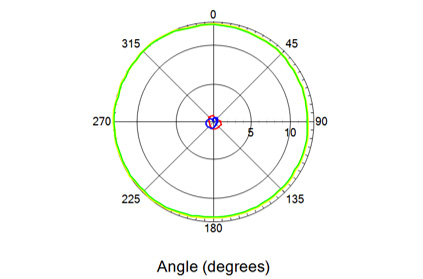
Rysunek 8. Wykres dla rotacji płaszczyźnie poziomej i w polaryzacji pionowej. Częstotliwość 1 [GHz].
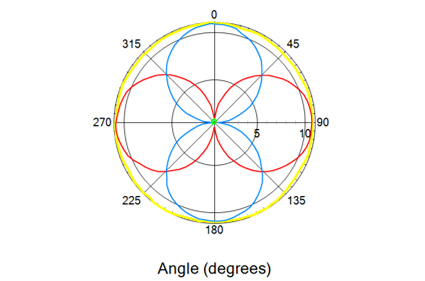
Rysunek 9. Wykres dla rotacji płaszczyźnie poziomej. Wszystkie Osie skierowane w górę. Częstotliwość 1 [GHz].
Wymagania komory kalibracyjnej
Aby poprawnie zmierzyć izotropowość komora kalibracyjna powinna spełniać założenia i posiadać konkretne parametry. W tym przypadku w tabelkę (tabela 2) poniżej przedstawiono takie kluczowe parametry.
| Wymaganie | Wartość |
|---|---|
| Jednorodność pola | sVSWR < +- 0,25 [dB] (omówiony później) |
| Wzmacniacze | Harmoniczne <-40 [dBc] (Stosunek mocy wyższej harmonicznej do mocy częstotliwości podstawowej) |
| Antena nadawcza | Polaryzacja ortogonalna <-30 [dB] |
| Statyw sondy | Powinien być taki sam jak w praktycznym użytkowaniu |
| Dokładność obrotowa sondy pola | < +- 1 stopień |
| Dokładność pozycjonera sondy | < +- 1 [mm] |
| Wpływ obrotnicy oraz statywu sondy | < -0,25 [dB] |
| Temperatura | Zmierzona podczas testu |
| Wilgotność | Zmierzona podczas testu |
Tabela 2. Parametry komory kalibracyjnej.
Na poniższych zdjęcia przedstawiamy komorę oraz sprzęt pomiary (rysunek 10 i 11).

Rysunek 10. Sprzęt pomiarowy.

Rysunek 11. Wnętrze obiektu.

Rysunek 12. Pomiar fali stojącej.
sVSWR (ang. Site Voltage Standing Wave Ratio) jest jednym z kluczowych parametrów komory. Pomiar ten wykonuje się z użyciem sondy pola umieszczonej na stole pomiarowym. Zgodnie z wymaganiami normy dokonuje się odczytu natężenia pola elektrycznego dla różnych położeń sondy na stole (co 10 [cm]).
Ideą tego typu testu jest poszukiwanie fal stojących, które mogą być obecne w komorze bezodbiciowej nawet zakładając jej perfekcyjne wykonanie oraz wysokiej jakości absorbery.
Przedstawiamy również fragment normy IEC 61000-4-3 przedstawiający metodę pomiarową (rysunek 13).

Rysunek 13. Fragment normy przedstawiający wykonywany test.
Dla poniższej metody pomiarowej możemy wyznaczyć w końcu wyniki sVSWR zgodnie z normą EN 61000-4-3. Poniższy wykres przedstawia taki pomiar z odchyleniem maksymalnym +- 0.5 [dB] w zakresie od -20 do 20 [cm] (rysunek 14).
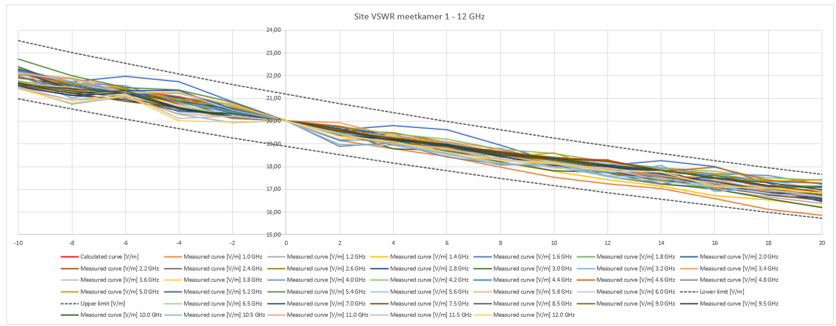
Rysunek 14. Pomiar sVSWR od 1 do 12 GHz na idealnym dielektryku.
Wykonany został też pomiar sVSWR przedstawiający wpływ styropianowego podłoża na rozkład pola. Niestety ale w tym przypadku sVSWR ma dwa przekroczenia (rysunek 15).
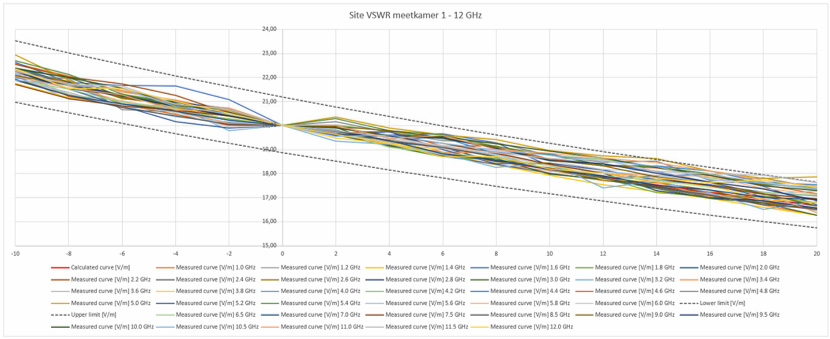
Rysunek 15. Pomiar sVSWR od 1 do 12 GHz na styropianie.
Wpływ anizotropowości na niepewność pomiarową
Nasuwa się następujące pytanie:
„Czy możemy zignorować anizotropię sondy pola jeśli jedną z osi sondy przyłożymy/wyrównamy do generowanego pola?”
Odpowiedź brzmi: niestety nie!
Poniżej znajduje się wykres przedstawiający pomiary 3 różnych sond w tej konfiguracji. Mamy tutaj różnicę w pomiarach na poziomie 8 [dB] (rysunek 16)!
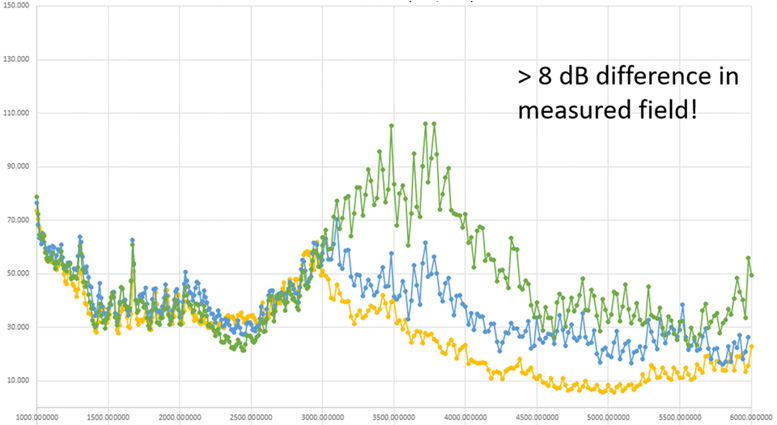
Rysunek 16. Anizotropowość i pomiary.
Kolejne pytanie, które należy zadać:
„Co powoduje ten efekt?”
Nawet przy zastosowaniu w pomiarze tylko jednej anteny w linii z generowanym polem, efekty odbiciowe komorzy EMC będą wpływać na sygnał dochodzący do sondy pod różnymi kątami (rysunek 17).
Norma EN61000-4-3 wspomina, że dla 75% z 16 punktów pomiarowych w polu jednorodnym, natężenie powinno być takie samo z odchyleniem od 0 do 6 dB. Należy też zauważyć, że błąd +-6 [dB] oznacza, że odbicia mają taką samą amplitudę jak generowana fala. Dla pozostałych 25% punktów wynik ten może być nawet gorszy. Sonda z dużą wartością izotropowości będzie mierzyć odbite sygnały z dużym błędem (zazwyczaj o wiele większe pole niż generowane).
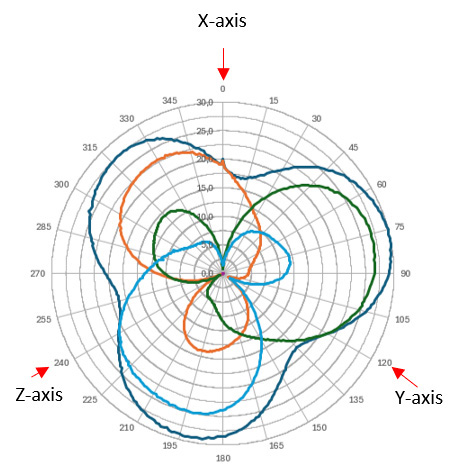
Rysunek 17. Wykres biegunowy przykładowego pomiaru.
Można więc założyć, że antena sondy pola przyłożona do generowanego pola i jej 50% anizotropowego błędu będzie nadal obecne w ogólnym budżecie. W tym przypadku anizotropia sondy 3.5 [dB] będzie wpływać na niepewność pomiarową w stopniu około 1.9 [dB] całej niepewności pomiarowej.
Przykład obliczeniowy wyliczenia anizotropii
Poniżej znajduje się przykładowe obliczenie anizotropii sondy pola:

Rysunek 18. Wzory do obliczenia anizotropii
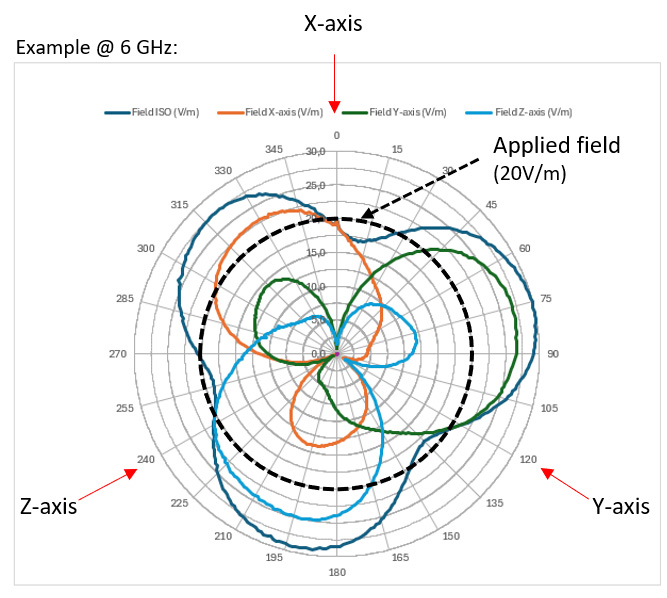
Rysunek 19. Wykres biegunowy dla niniejszego przypadku
Spróbujmy więc wyliczyć całkowitą niepewność pomiarową. Całkowita niepewność pomiarowa jest wartością RSS (z ang. Root Sum Square). Można ją zapisać poniższym równaniem:
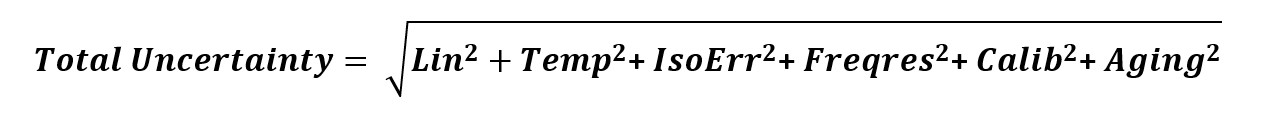
gdzie:
- Lin – błąd liniowości,
- Temp – błąd powodowany przez temperaturę,
- IsoErr – błąd izotropowy,
- Freqres – niepewność pomiarowa częstotliwości,
- Calib – niepewność pomiarowa kalibracji (z laboratorium kalibracyjnego),
- Aging – dokładność sondy (stabilność, odpowiedź temperaturowa itd.).
Załóżmy więc:
- błąd liniowości – 0,5 [dB],
- błąd powodowany przez temperaturę – 0,5 [dB],
- błąd izotropowy – 1.9 [dB],
- niepewność pomiarowa częstotliwości – 0 [dB],
- niepewność pomiarowa kalibracji (z laboratorium kalibracyjnego) – 1,2 [dB],
- dokładność sondy (stabilność, odpowiedź temperaturowa itd.) 1 [dB].
Wtedy całkowita niepewność pomiarowa wyniesie: 2,55 [dB].
Należy zauważyć, że błąd anizotropii jest dominującym źródłem niepewności pomiarowej! Oznacza to, że musimy dążyć do sondy, która będzie miała jak najmniejszą niepewność pomiarową (najlepiej poniżej 1 [dB])!
Dodatkowa uwaga!
Niepewność pomiarowa kalibracji jest stosowana, gdy współczynniki korekcyjne są stosowane w sondzie pola.
Możemy wspomnieć jeszcze o współczynnikach korekcyjnych sondy pola. Kalibracja sondy polega na wygenerowaniu znanego pola elektrometrycznego (dla znanego zakresu częstotliwości) i skierowaniu jednej z osi sondy równolegle. Procedurę powtarza się dla każdej osi X, Y i Z.
Dla każdej z osi współczynniki korekcyjne dla poszczególnych osi wyznacza się liniowo wzorem:
Kx(f) = Egen(f)/Emesx(f)
Ky(f) = Egen(f)/Emesy(f)
Kz(f) = Egen(f)/Emesz(f)
gdzie:
- Egen(f) – generowane natężenie pola (wiadome),
- Emesx(f), Emesy(f), Emesz(f) – zmierzone natężenie pola przez konkretną oś sondy.
Można je też wyznaczyć w formie logarytmicznej (dB) stosując formułę:
Kxlog(f) = 20log * Kx(f)
Kylog(f) = 20log * Ky(f)
Kzlog(f) = 20log * Kz(f)
By uzyskać dokładny odczyt stosując współczynniki korekcyjne możemy uzyskać poprawny wynik mierzonego pola dla poszczególnych osi. Zapisać to można równaniem:
Excor = Exmer * Kx
Eycor = Eymer * Ky
Ezcor = Ezmer * Kz
gdzie:
- Kx, Kx, Kx - współczynniki korekcyjne,
- Exmer, Eymer, Ezmer - zmierzone wartości pola dla poszczególnych osi.
Na koniec możemy wyznaczyć sumę kwadratów generowanego pola wzorem:
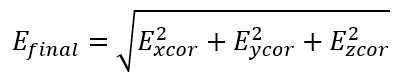
Podsumujmy:
- By otrzymać dobrze zmierzone wartości pola anizotropowość powinna być tak niska jak to możliwe (najlepiej poniżej 1 [dB]).
- Anizotropia silnie wzrasta wraz z wzrostem częstotliwości.
- Poniżej 1 [GHz] anizotropowość jest prawie idealna. Jest to powodowane małymi wymiarami sondy pola w porównaniu do długości fali.
- Izotropowość musi być wyspecyfikowana dla całego zakresu częstotliwości sondy pola.
Przykładowe pomiary anizotropii sond pola elektrycznego
Weźmy dla przykładu sondę pola marki „X”. Jak widać powyżej 1 [GHz] anizotropia sondy wynosi około 0.7 [dB], ale współczynnik ten bardzo wzrasta do drastycznych 4 [dB] przy 6 [GHz] (rysunek 20).
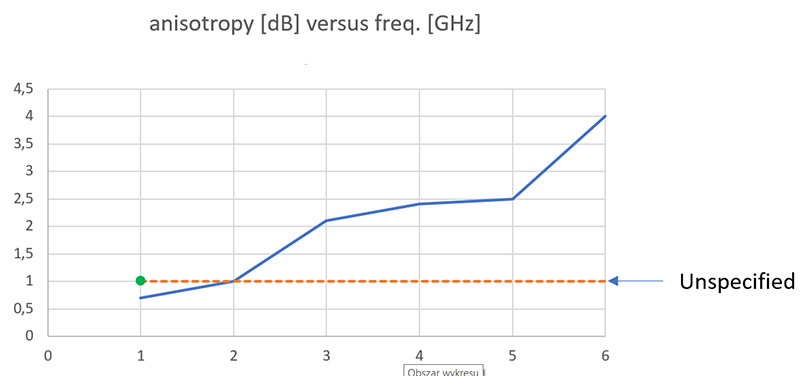
Rysunek 20. Anizotropowość sondy pola marki "X".
W przypadku sondy RS10i anizotropowość sondy wyniosła 1 [dB] dla 10 [GHz] (rysunek 21).
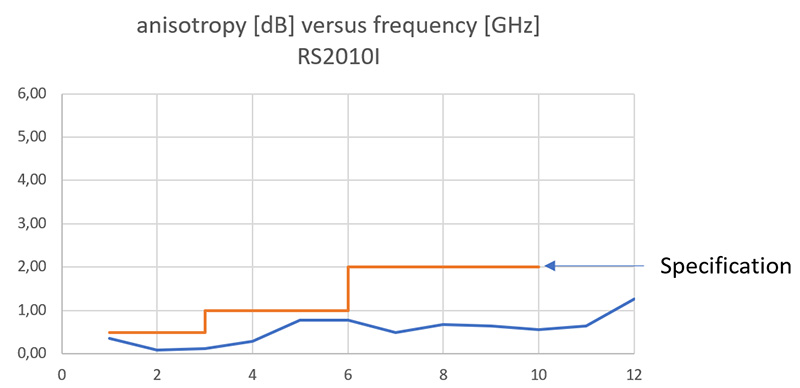
Rysunek 21. Anizotropowość sondy pola Raditeq RS10I.
Jeszcze lepsze wyniki otrzymaliśmy dla sondy RS40. Dla tego przykładu anizotropia jest niska dla całego zakresu częstotliwości (rysunek 22)!
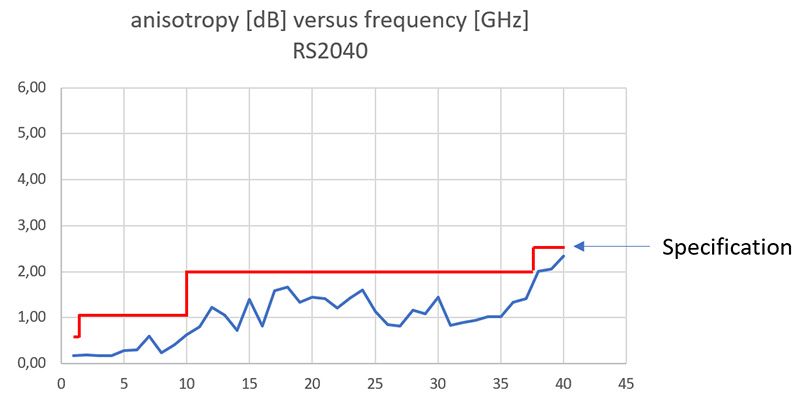
Rysunek 22. Anizotropowość sondy pola Raditeq RS40.
Autorem prezentacji, na której to bazuje artykuł jest Koen Pepping z firmy Raditeq.

